In the realm of artificial intelligence, the larger the scale, the stronger the capability seems to be. In pursuit of more powerful language models, major tech companies are madly stacking model parameters and training data, only to find that costs are skyrocketing as well. Is there no method that is both economical and efficient for training language models?
Researchers from Harvard University and Stanford University recently published a paper in which they discovered that the precision of model training acts like a hidden key, unlocking the "cost code" of language model training.
What is model precision? Simply put, it refers to the number of digits used in model parameters and computational processes. Traditional deep learning models typically use 32-bit floating-point numbers (FP32) for training, but in recent years, with the advancement of hardware, it has become possible to use lower-precision numeric types, such as 16-bit floating-point numbers (FP16) or 8-bit integers (INT8) for training.
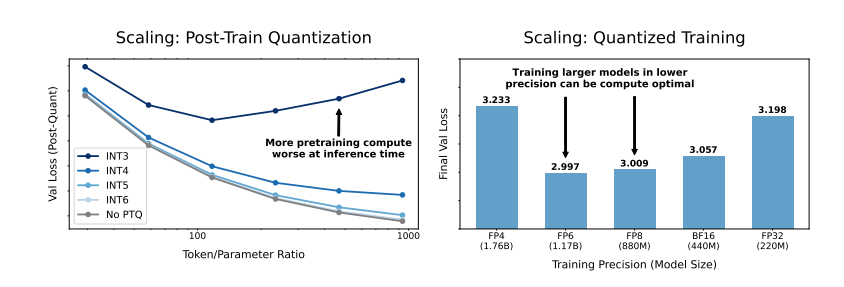
So, what impact does reducing model precision have on model performance? This is precisely the question this paper seeks to explore. Through extensive experiments, the researchers analyzed the cost and performance changes of model training and inference under different precisions, and proposed a new set of "precision-aware" scaling rules.
They found that training with lower precision can effectively reduce the "effective number of parameters" of the model, thereby reducing the computational load required for training. This means that with the same computational budget, we can train larger-scale models, or at the same scale, using lower precision can save a significant amount of computational resources.
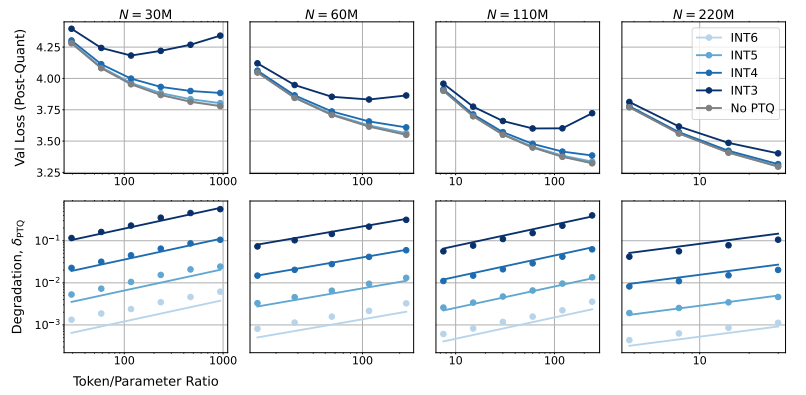
More surprisingly, the researchers also found that in some cases, training with lower precision can actually improve model performance! For example, for models that require "post-training quantization," using lower precision during training makes the model more robust to the reduction in precision after quantization, thereby performing better during inference.
So, what precision should we choose for training models? Through analyzing their scaling rules, the researchers came to some interesting conclusions:
Traditional 16-bit precision training may not be the optimal choice. Their studies suggest that 7-8-bit precision might be a more economical and efficient option.
Pursuing ultra-low precision (such as 4-bit) training is also not wise. At extremely low precision, the effective number of parameters of the model will plummet, and to maintain performance, we need to significantly increase the model size, which in turn leads to higher computational costs.
The optimal training precision may vary for models of different scales. For models that require extensive "overtraining," such as the Llama-3 and Gemma-2 series, using higher precision for training may be more economical and efficient.
This research provides a fresh perspective on understanding and optimizing language model training. It tells us that the choice of precision is not static but needs to be balanced according to specific model scales, training data volumes, and application scenarios.
Of course, this study also has some limitations. For example, the model sizes they used were relatively small, and the experimental results may not be directly applicable to larger-scale models. Additionally, they focused only on the model's loss function and did not evaluate the model's performance on downstream tasks.
Nevertheless, this research remains significant. It reveals the complex relationship between model precision and model performance and training costs, and provides valuable insights for designing and training more powerful and economical language models in the future.
