Recently, large language models (LLMs) have shown impressive performance across various tasks, effortlessly writing poetry, coding, and chatting – they seem to be capable of anything! But can you believe it? These "genius" AIs are actually "math novices"! They often struggle with simple arithmetic problems, leaving people astonished.
A recent study revealed the quirky secret behind the arithmetic reasoning abilities of LLMs: they neither rely on powerful algorithms nor solely on memory, but instead employ a strategy known as "heuristic hodgepodge"! It's like a student who hasn’t studied mathematical formulas and theorems seriously but relies on a bit of "cleverness" and "rules of thumb" to guess the answers.
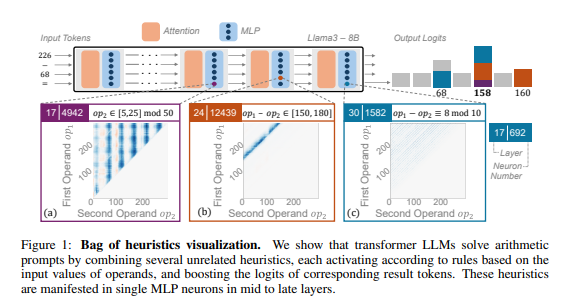
Researchers focused on arithmetic reasoning as a typical task and conducted an in-depth analysis of several LLMs, including Llama3, Pythia, and GPT-J. They discovered that the part of the LLM responsible for arithmetic calculations (referred to as the "circuit") is composed of many individual neurons, each acting like a "mini-calculator" that is responsible for recognizing specific numerical patterns and outputting corresponding answers. For example, one neuron might be dedicated to identifying "numbers with a unit digit of 8," while another neuron might focus on recognizing "subtraction operations that result in values between 150 and 180."
These "mini-calculators" are like a jumble of tools; LLMs do not use them according to a specific algorithm but instead combine these "tools" randomly based on the input numerical patterns to calculate answers. It’s akin to a chef who, without a fixed recipe, improvises with whatever ingredients are available, ultimately creating a "mystery dish."

Even more surprisingly, this "heuristic hodgepodge" strategy emerged early in the training of LLMs and was gradually refined as training progressed. This means that LLMs have relied on this "patchwork" reasoning method from the very beginning, rather than developing this strategy later on.
So, what issues might this "quirky" arithmetic reasoning method lead to? Researchers found that the generalization capability of the "heuristic hodgepodge" strategy is limited and prone to errors. This is because the "cleverness" that LLMs possess is finite, and these bits of "cleverness" may themselves have flaws, causing them to fail to provide correct answers when encountering new numerical patterns. It's like a chef who can only make "tomato scrambled eggs" being suddenly asked to prepare "fish-flavored shredded pork"; they would undoubtedly be flustered and at a loss.
This study reveals the limitations of LLMs' arithmetic reasoning abilities and points to directions for future improvements in their mathematical capabilities. Researchers believe that merely relying on existing training methods and model architectures may not be sufficient to enhance LLMs' arithmetic reasoning abilities; new approaches need to be explored to help LLMs learn stronger and more generalized algorithms, enabling them to truly become "math experts."
Paper link: https://arxiv.org/pdf/2410.21272










