在人工智能的世界里,大型语言模型(LLMs)以其卓越的自然语言处理能力而著称。然而,这些模型在实际应用中的部署却面临着巨大的挑战,主要是因为它们在推理阶段的高计算成本和内存占用。为了解决这一问题,研究人员们一直在探索如何提高LLMs的效率。最近,一种名为Q-Sparse的方法引起了广泛关注。
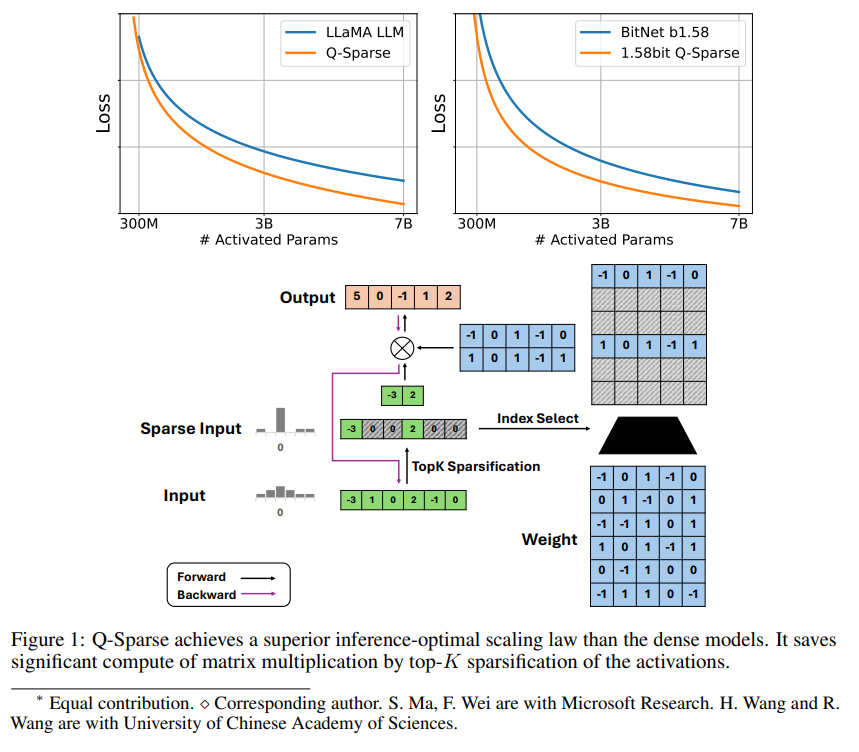
Q-Sparse是一种简单但有效的方法,它通过在激活中应用top-K稀疏化和训练中的直通估计器,实现了LLMs的完全稀疏激活。这意味着在推理时可以显著提高效率。关键的研究成果包括:
Q-Sparse在保持与基线LLMs相当的结果的同时,推理效率更高。
提出了一种适用于稀疏激活LLMs的推理最优扩展法则。
Q-Sparse在不同设置中均有效,包括从头开始训练、现成LLMs的继续训练和微调。
Q-Sparse适用于全精度和1位LLMs(例如BitNet b1.58)。
稀疏激活的优势
稀疏性通过两种方式提高LLMs的效率:首先,稀疏性可以减少矩阵乘法的计算量,因为零元素不会被计算;其次,稀疏性可以减少输入/输出(I/O)的传输量,这是LLMs推理阶段的主要瓶颈。
Q-Sparse通过在每个线性投影中应用top-K稀疏化函数来实现激活的全稀疏性。对于反向传播,使用直通估计器计算激活的梯度。此外,还引入了平方ReLU函数来进一步提高激活的稀疏性。
实验验证
研究人员通过一系列扩展实验研究了稀疏激活LLMs的扩展法则,并得出了一些有趣的发现:
稀疏激活模型的性能随着模型大小和稀疏比率的增加而提高。
给定固定的稀疏比率S,稀疏激活模型的性能与模型大小N呈幂律扩展法则。
给定固定的参数N,稀疏激活模型的性能与稀疏比率S呈指数律扩展法则。
Q-Sparse不仅可以用于从头开始训练,还可以用于现成LLMs的继续训练和微调。在继续训练和微调设置中,研究人员使用与从头开始训练相同的架构和训练过程,唯一的区别是使用预训练权重初始化模型,并启用稀疏函数继续训练。
研究人员正在探索将Q-Sparse与1位LLMs(如BitNet b1.58)和混合专家(MoE)结合使用,以进一步提高LLMs的效率。此外,他们还在努力使Q-Sparse与批量模式兼容,这将为LLMs的训练和推理提供更多的灵活性。









